Digitale Ausgabe
Download
| TEI-XML (Ansicht) | |
| Text (Ansicht) | |
| Text normalisiert (Ansicht) |
Ansicht
| Textgröße | |
| Originalzeilenfall ein/aus | |
| Zeichen original/normiert | |
Tafeln
Zitierempfehlung
Alexander von Humboldt, Joseph Louis Gay-Lussac: „Observations sur l’intensité et l’inclinaison des forces magnétiques, faites en France, en Suisse, en Italie et en Allemagne“, in: ders., Sämtliche Schriften digital, herausgegeben von Oliver Lubrich und Thomas Nehrlich, Universität Bern 2021. URL: <https://humboldt.unibe.ch/text/1807-Observations_sur_l-1> [abgerufen am 20.04.2024].
URL und Versionierung
|
Permalink: https://humboldt.unibe.ch/text/1807-Observations_sur_l-1 |
| Die Versionsgeschichte zu diesem Text finden Sie auf github. |
| Titel | Observations sur l’intensité et l’inclinaison des forces magnétiques, faites en France, en Suisse, en Italie et en Allemagne | ||||
|---|---|---|---|---|---|
| Jahr | 1807 | ||||
| Ort | Paris | ||||
|
Nachweis in: Mémoires de physique et de chimie, de la Société d’Arcueil 1 (1807), S. 1–22, Tafel.
|
|||||
| Beteiligte | Joseph Louis Gay-Lussac | ||||
| Sprache | Französisch | ||||
| Typografischer Befund | Antiqua; Auszeichnung: Kursivierung; Fußnoten mit Ziffern; Tabellensatz; Formelsatz; Besonderes: mathematische Sonderzeichen. | ||||
|
Identifikation |
|||||
Statistiken
|
|||||
| Weitere Fassungen | |
|---|---|
|
|
Observations sur l’intensité et l’inclinaison des forces magnétiques, faites en France, en Suisse, en Italie et en Allemagne (Paris, 1807, Französisch) |
|
|
Beobachtungen über die Stärke und über die Neigung der magnetischen Kräfte, angestellt in Frankreich, der Schweiz, Italien und Deutschland (Halle, 1808, Deutsch) |
OBSERVATIONS sur l’intensité et l’inclinaison des forcesmagnétiques, faites en France, enSuisse, en Italie et en Allemagne: Par MM. A. de Humboldt et Gay-Lussac. Lu à l’Institut le 8 septembre 1806.
Les causes et les lois du magnétisme terrestresont restées dans la plus grande obscurité, aumilieu des progrès rapides que la physique vientde faire. |2| Les variations tant diurnes que séculaires del’aiguille aimantée, son inclinaison et sa dé-clinaison sur les principaux points du globe;l’intensité des forces magnétiques, le nombreet le cours des bandes sans déclinaison, nesont encore que très-peu connus. Les obser-vations des voyageurs et des physiciens, quid’ailleurs ne portent presque uniquement quesur la déclinaison de l’aiguille aimantée, ontété faites à des époques trop éloignées les unesdes autres, et en employant des instrumens oudes méthodes trop peu exacts, pour qu’il soitpossible d’asseoir sur elles les bases d’une théo-rie qui embrasseroit les divers phénomènes dumagnétisme terrestre. Le desir de concourir àfournir quelques matériaux pour l’avancementde cette partie de nos connoissances, nous aengagés, M. Humboldt et moi, dans une suited’observations sur l’inclinaison et l’intensité desforces magnétiques. Nous nous en sommes oc-cupés dans un voyage d’une année, que nousavons fait en France, en Suisse, en Italie eten Allemagne, et dans lequel j’ai pu profiterdes vastes connoissances de mon ami. Ce sontces observations que nous avons l’honneur deprésenter aujourd’hui à l’Institut. Le courtespace de tems dans lequel elles ont été faites |3| et qui les rend presque simultanées; la grandeétendue qu’elles embrassent, et, nous osonsle dire, leur exactitude, nous font espérerqu’il les accueillera avec intérêt (1). La boussole dont nous nous sommes servispour déterminer les inclinaisons magnétiquesest celle de Borda. Elle avoit été exécutée parM. Lenoir, pour l’expédition d’Entrecasteaux,et nous avoit été confiée par S. E. le ministrede la marine. Celle pour les oscillations ho-risontales consistoit en une aiguille aimantée,parallélogrammique, suspendue à un fil desoie plate. Une boîte, dont deux faces oppo-sées étoient en verre, servoit à la garantir desagitations de l’air. La simplicité de cet ins-trument, la grande exactitude à laquelle onpeut atteindre par son moyen, et la méthodedue à Borda de conclure des oscillations del’aiguille la force qui les produit, sont aujour-d’hui connues de tout le monde. Il n’en estpeut-être pas de même de la meilleure manièrede déterminer pour un lieu l’inclinaison etl’intensité des forces magnétiques: les opinionsne nous paroissent pas encore fixées à cet
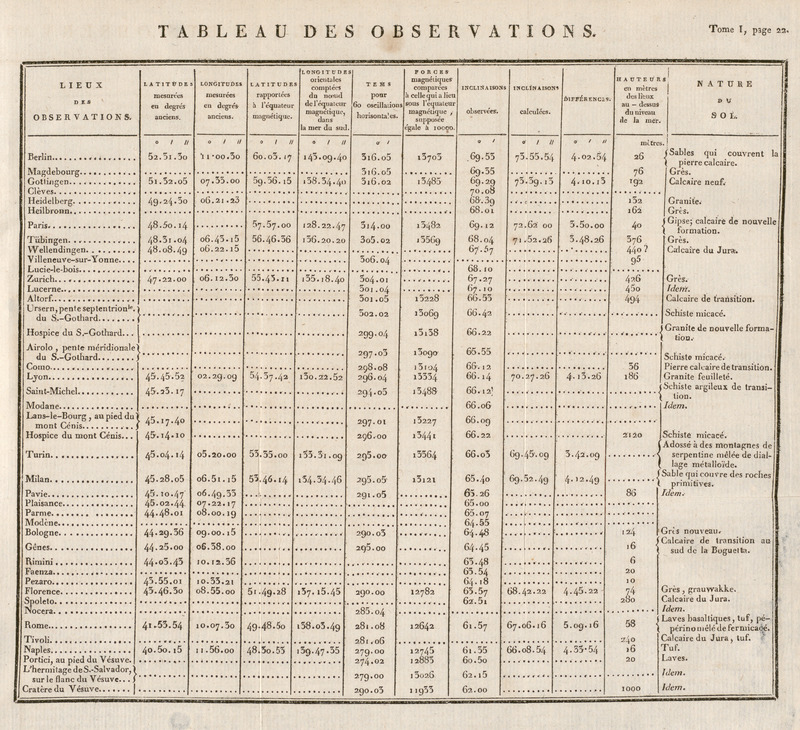
(1) Toutes nos observations ont été faites entre le15 mars 1805 et le 1er. mai 1806.|4| égard, et c’est pour cela que nous croyonspouvoir nous permettre les détails dans lesquelsnous allons entrer. Lorsqu’une aiguille d’inclinaison est dans sonméridien magnétique, une variation de po-sition à droite ou à gauche de ce plan produitune augmentation dans l’inclinaison. On peutdonc, pour déterminer le méridien magné-tique, chercher le plan pour lequel l’inclinaisonde l’aiguille est un minimum; mais ce procédén’a point la simplicité qu’il paroît avoir aupremier abord, et nous allons voir qu’il enexiste un autre plus exact et plus expéditif. Si on conçoit une aiguille d’inclinaison dansun plan perpendiculaire à son méridien, laforce horisontale qui est une des composantesde la force magnétique étant alors sans effet,l’aiguille se tiendra verticale. La position dece plan est extrêmement facile à déterminer;parce que, sans attendre que l’aiguille soitarrivée au repos, on peut juger si ses oscil-lations de part et d’autre de la verticale quipasse par son centre de suspension sont égales,et par conséquent la faire tourner si elles nele sont pas. Il ne faut alors qu’un très-petitmouvement; car la force horisontale croissantcomme le sinus de l’angle de déviation, il |5| en résulte une variation très-sensible dans ladirection de l’aiguille. Le plan perpendiculaireau méridien magnétique étant ainsi trouvé, ilest facile d’en conclure ce dernier et d’y dé-terminer ensuite l’inclinaison; mais l’aiguillepouvant, à cause du frottement, rester un peuau-dessus ou au-dessous de sa vraie direction,il sera nécessaire de faire plusieurs observationspour en prendre la moyenne. Telles seroient les opérations à faire pourtrouver l’inclinaison si l’aiguille étoit parfaite.Il s’en faut de beaucoup qu’elle le soit ordi-nairement, et de là naissent plusieurs causesd’erreur qu’il faut chercher à corriger. Voicien peu de mots comment on peut y parvenir. Le centre de gravité de l’aiguille pouvant setrouver hors de son axe de suspension et desa ligne de figure, le plan méridien n’est pluscelui qui seroit perpendiculaire au plan danslequel elle se tient verticale. Il se détermineen faisant tourner la boussole jusqu’à ce quel’aiguille prenne de nouveau une directionverticale, et en divisant en deux parties égalesl’angle décrit. L’inclinaison a de même besoind’une correction. Si le centre de gravité del’aiguille est au-dessus du centre de suspension,l’inclinaison est trop petite; s’il est au-dessous |6| elle est trop grande. Mais en changeant lespôles de l’aiguille, les effets des causes per-turbatrices sont alors en sens contraire, et lamoyenne de toutes les observations donne lavraie inclinaison. Il n’est cependant pas né-cessaire de renverser les pôles chaque fois qu’onveut la déterminer. Quand la correction estconnue pour un lieu, on peut la regarder, sanserreur sensible, comme constante pour unautre qui seroit peu éloigné du premier, ensupposant d’ailleurs que l’aiguille n’éprouve pasde changemens. M. Laplace a proposé une autre méthodeégalement simple pour déterminer l’inclinaison.En nommant M et P les nombres d’oscillationsfaites dans le même tems par l’aiguille dans leméridien magnétique et dans le plan qui luiest perpendiculaire, l’inclinaison I est donnéepar la formule sin \( I=\frac{P^2}{M^2} \) Comme cette méthode est fondée sur les os-cillations dont on peut mesurer rigoureusementle tems, nous sommes convaincus qu’elle peutdonner une très-grande précision; mais nousavons à regretter que notre aiguille n’ayantpas beaucoup de grandeur et une mobilitéparfaite, il ne nous ait pas été possible de |7| compter un assez grand nombre d’oscillationspour l’employer avec succès. L’intensité des forces magnétiques se déter-mine en faisant osciller l’aiguille d’inclinaisondans son méridien, et en prenant pour sa mesurele carré du nombre d’oscillations faites dans untems donné. Il peut arriver cependant que l’ai-guille éprouve une altération, et dans ce castoutes les observations seroient affectées d’uneerreur qui pourroit être considérable. On peut,il est vrai, changer les pôles de l’aiguille etl’aimanter à saturation; mais les différencesqu’on observe dans ses oscillations, quand ellea été ainsi aimantée deux fois en sens contraire,sont souvent assez grandes pour que, dans cesexpériences qui démandent de l’exactitude, onne puisse se permettre de faire ces changemens. La méthode que nous avons employée nousparoît à l’abri de tout inconvénient. Elle consisteà se servir des oscillations d’une aiguille hori-sontale suspendue à un fil, pour en conclureensuite, lorsque l’inclinaison est donnée, cellesqu’elle feroit dans sa vraie direction. Soit F laforce magnétique totale pour un lieu déterminé, I l’inclinaison et N le nombre d’oscillations ho-risontales faites pendant le tems T; \( \frac{N}{T\sqrt{(\text{cos}\;I)}} \) |8| sera le nombre d’oscillations faites par l’aiguilledans sa vraie direction, pendant l’unité detems. Et si on veut comparer tout de suitel’intensité de la force magnétique avec celle F′ d’un autre endroit, on aura \( \frac{F}{F'}=\frac{N^2}{T^2\cos I}\times\frac{T'^2\cos I'}{N'^2} \) Tels sont les moyens que nous avons em-ployés pour déterminer l’inclinaison et l’intensitédes forces magnétiques dans les divers lieux quenous avons parcourus. Tous nos résultats ontété réunis dans un tableau particulier, et voicidans quel ordre ils y ont été disposés. La pre-mière colonne comprend les noms des lieux;leur latitude et leur longitude forment la se-conde et la troisième. Pour comparer nosobservations sur l’inclinaison aux résultats dela théorie, d’après les formules que M. Biot a publiées (1), nous avons ramené les latitudeset longitudes terrestres à l’équateur et au mé-ridien magnétiques déterminés l’un et l’autre,d’après les observations de MM. Lapeyrouse et Humboldt, en Amérique. Ce sont ces lati-tudes et longitudes qui forment la quatrième
(1) Journal de Physique, tom. 59.|9| et la cinquième colonnes de notre tableau. Lahuitième renferme les inclinaisons observées;la neuvième celles qui ont été calculées, etla dixième les différences des unes aux autres.Dans la sixième colonne on trouve, expriméen secondes, le tems qu’il a fallu dans chaquelieu à notre aiguille horisontale pour faire 60oscillations, et dans la septième les intensitéstotales correspondantes. Pour comparer cesdernières entre elles, nous avons pris pourterme de comparaison l’intensité des forces sousl’équateur magnétique, et nous l’avons sup-posée égale à 10000. Nous nous sommesservis, pour cet objet, des observations del’un de nous, desquelles il résulte qu’une ai-guille d’inclinaison qui feroit 245 oscillationsà Paris, n’en feroit plus que 211 sous l’équa-teur magnétique pendant le même espace detems. Connoissant l’inclinaison à Paris et lesoscillations de notre aiguille horisontale, ilnous a été facile, d’après ce que nous avonsdit, de calculer ses oscillations dans sa vraiedirection, et par suite celles qu’elle feroit sousl’équateur magnétique; car en supposant égauxles rapports des intensités donnés par deuxaiguilles dans deux lieux différens, on dé-montre que leurs nombres d’oscillations dans ces |10| mêmes lieux, pendant le même tems, sontproportionnels entre eux. En faisant nos observations, nous avons eusoin en même tems de reconnoître la naturedu sol et son élévation au-dessus du niveau dela mer. Il y a des roches qui, par leur nature,ne peuvent avoir aucune influence sur l’aiguilleaimantée; mais il en est d’autres, telles queles basaltes et les serpentines, qui renfermentquelquefois beaucoup de fer, et qui peuventalors en avoir une très-forte. Il a été reconnuqu’à des hauteurs bien plus considérables quecelles auxquelles on peut s’élever sur les mon-tagnes, la force magnétique ne varie pas sen-siblement, et d’après cela, il seroit inutile detenir compte de l’élévation des lieux. Elle pour-roit cependant donner une idée de l’influencequ’ils auroient sur l’aiguille, s’ils recéloient dufer. Mais outre cela, la constitution d’un paysdépendant tout aussi bien de sa hauteur quede sa position géographique, il nous a parud’autant plus utile de rapporter tout ce quipeut la faire connoître, que jusqu’à présentcet objet a été trop négligé. Ainsi donc l’éléva-tion du sol au-dessus du niveau de la mer etsa nature, occuperont dans notre tableau deuxcolonnes séparées. |11| Lorsque nous sommes partis de Paris, nosinstrumens, que nous n’avions pu avoir à notredisposition que la veille du jour de notre dé-part, ne nous ont pas permis d’y déterminerl’inclinaison et l’intensité des forces magné-tiques. Nous n’avons pu commencer nos ob-servations qu’à Villeneuve-sur-Yonne, mais delà nous les avons continuées sur tous les pointsde notre passage qui pouvoient mériter quelqueattention. J’observerai cependant que les ré-sultats que j’ai obtenus à Paris, sur l’intensitédes forces magnétiques, un an après en êtreparti, doivent être, relativement à l’aiguille,en parfaite harmonie avec les autres; car ayantpassé deux fois à Milan, à six mois d’inter-valle, nous avons trouvé que notre aiguille yfaisoit exactement le même nombre d’oscilla-tions la seconde fois que la première, soit dansl’intérieur de la ville, soit hors ses murs. Nos observations sur l’intensité des forcesmagnétiques à Turin, influencées sans doute parquelque cause très-particulière, nous ayantparu quelque tems après s’écarter beaucoup ensens contraire de la loi que suivoient les autres,nous avons fait osciller une nouvelle aiguilleà Milan, comparativement avec la nôtre, etnous l’avons envoyée à M. Vassali, qui a eu |12| la complaisance de compter ses oscillations endivers endroits dans l’intérieur et à l’extérieurde Turin. C’est d’après ses résultats et ceux quenous avions obtenus à Milan que nous avonscalculé les oscillations que notre aiguille auroitfaites dans la première de ces villes. Nous devons faire remarquer encore, avantd’aller plus loin, quel est le degré de préci-sion auquel on peut atteindre dans ce genred’expériences, afin qu’on ne se méprenne passur de légères anomalies qui pourroient setrouver dans nos résultats. D’abord, pour lesinclinaisons, avec un instrument de 0m,07 derayon, il seroit difficile, même dans le calmele plus parfait, de les déterminer à plus desix minutes près. Dans un voyage, dans lequelon n’a pas toujours ni le tems ni les commo-dités qu’on pourroit desirer, les limites deserreurs doivent être un peu plus éloignéesentre elles. Nous croyons néanmoins que lesplus grands écarts de nos observations, prin-cipalement de celles que nous avons faites enallant de Rome à Berlin, ne s’étendent pas au-delà de 10 minutes. Relativement à l’influencedes localités particulières, on ne peut assurerjusqu’où elle peut s’étendre, quoique, en gé-néral, elle doive être assez petite. Nous n’avons |13| pu toujours observer en plein air, et quandnous avons été obligés de le faire à couvert,nous avons choisi les appartemens les plusgrands, en évitant ceux où nous découvrionsquelque masse de fer un peu considérable. Pour les oscillations horisontales, nous pou-vons répondre de leur parfaite exactitude. Nousen avons toujours mesuré le tems avec un chro-nomètre de M. Berthoud, et d’ailleurs il n’ya rien de plus facile que de les observer. Dansle même endroit, elles présentent toujours leplus grand accord. Si, comparées dans deslieux différens, elles paroissent quelquefois nepas suivre une loi parfaitement régulière, c’estdans les localités qu’il faut en chercher la cause. Maintenant que nous avons exposé commentnous avons fait nos observations, ainsi que lamanière de les réduire et de les comparer lesunes aux autres, nous allons passer aux ré-sultats qu’elles nous ont présentés. Un des principaux buts que nous nous étionsproposés dans notre voyage, étoit de nousassurer si la haute chaîne des Alpes pouvoitavoir de l’influence sur l’intensité et l’inclinaisondes forces magnétiques. Nous l’avons traverséedeux fois en deux endroits différens, la pre-mière au Mont-Cenis, entre Lyon et Turin; |14| la seconde au St.-Gothard, entre Come et Al-torf. En fixant les yeux sur le tableau, on voitque, lorsque l’inclinaison est à Lyon 66° 14′,elle est à Chambéry, à St.-Michel et à Modane,presque à la même latitude, et dans la chaînemême, 66° 12′, 66° 12′ et 66° 6′; qu’àLanslebourg, qui est au pied du Mont-Cenis,elle est 66° 9′, et qu’enfin sur cette montagne,à l’Hospice et à la hauteur de 2120m on latrouve 66° 22′. A Turin, de l’autre côté dela chaîne des Alpes, nous l’avons observéede 66° 3′, c’est-à-dire de 9′ plus petite qu’àLyon; mais aussi cette dernière ville est unpeu plus au nord que la première. Si, sur leMont-Cenis, l’inclinaison paroît un peu plusforte qu’elle ne devroit l’être, en la comparantà celles des lieux voisins, à Chambéry, àSt.-Michel, à Modane et à Lanslebourg, quisont également dans la chaîne, elle paroît êtretelle à-peu-près qu’elle devroit être en raisonde leur position géographique seulement. Onne peut donc tirer aucune conséquence de cettefoible augmentation d’inclinaison dans un seulendroit, d’autant plus que sur le St.-Gothard,à une hauteur égale, nous avons trouvé, aucontraire, une inclinaison un peu plus foiblequ’à Airolo et à Ursern, situés l’un à la pente |15| méridionale de cette montagne, et l’autre à sapente septentrionale. En considérant à présent l’influence des Alpes sur l’intensité des forces magnétiques, nousla trouverons en général très-foible, si mêmeelle existe. A Lyon, l’intensité est à-peu-près lamême qu’à Turin. Sur le Mont-Cenis elle estun peu plus forte que dans ces deux villes;mais à Lanslebourg, au contraire, elle est plusfoible. A l’hospice du St.-Gothard, nous l’a-vons trouvée de 0,005 environ plus grandequ’à Airolo et à Ursern, et plus petite de 0,01qu’à Altorf. Il faut bien d’ailleurs accorderquelque chose pour les erreurs des observa-tions, car une erreur de quelques minutesdans l’inclinaison en produit une de plusieursmillièmes dans l’intensité. Il est permis outrecela de croire, jusqu’à ce qu’on ait prouvéle contraire, que l’inclinaison éprouve demême que la déclinaison, des variations auxdifférentes heures du jour et de la nuit. Mais,en admettant même qu’il y ait une différencedue à l’influence des Alpes, elle ne va qu’àun centième lorsqu’on compare quelques en-droits du milieu de la chaîne à ceux quien sont éloignés, et pour d’autres elle estencore plus petite. Nous croyons donc pouvoir |16| conclure que la chaîne des Alpes, au moinsdans les endroits où nous l’avons traversée,a une influence peu sensible sur l’inclinaisonet l’intensité des forces magnétiques. Pendant notre séjour sur le Mont-Cenis,où nous étions occupés d’expériences particu-lières, nous avons voulu voir si l’intensité desforces magnétiques n’éprouvoit pas de variationssensibles aux différentes heures du jour et dela nuit. Nous avons fait faire 250 oscillationsà notre aiguille, mais le tems de 1234″ qu’ellesont employé n’a jamais varié de plus d’uneseconde au-dessus ou au-dessous de ce nombre.A Rome, où nous avons encore fait un grandnombre d’expériences de ce genre, nous avonsobtenu des résultats semblables. D’après cela,il nous paroît évident que la force magnétiquene varie pas sensiblement en intensité pendantle jour ou pendant la nuit (1). Nous observeronspour ceux qui voudroient s’occuper de cetobjet, qu’on peut s’épargner l’ennui de compterà chaque observation toutes les oscillations;
(1) En supposant tous les phénomènes magnétiquesdépendans les uns des autres, on pourroit aussi en con-clure que l’inclinaison n’éprouve pas de variations appré-ciables; celles de la déclinaison étant déja très-petites.|17| car en prenant une aiguille très-paresseuse etdont le tems, pour chaque oscillation, seroitsupposé plus long que les variations qu’oncherche à évaluer, on peut employer le moyendont se servent les astronomes pour observerles révolutions des taches du soleil. Pendant le court espace de tems que nousavons passé dans Naples, nous avons été té-moins du violent tremblement de terre, du26 juillet 1805, et de l’éruption du Vésuve,du 12 août de la même année. Nous noussommes empressés de voir quels pourroientêtre les effets de ce volcan sur l’intensité etl’inclinaison des forces magnétiques. On saitque dans les produits des éruptions volca-niques, il y a quelquefois beaucoup de ferpeu oxidé qui agit fortement sur l’aiguille ai-mantée. Il étoit naturel d’après cela d’attribueraux volcans une très-grande influence, maisnous allons voir que pour le Vésuve elle esttrès-bornée. A Naples, qui est à environ deux lieues dece volcan, nous avons trouvé l’inclinaison égaleà 61° 35′. En suivant la marche des inclinai-sons depuis des endroits situés beaucoup plusau nord, on les voit décroître jusqu’à Naples,suivant une loi assez régulière. A Portici, qui |18| s’est élevé sur les ruines d’Herculanum, et quiest traversé par des courans de laves, nousavons observé l’inclinaison de 60° 50′. A l’her-mitage de S.-Salvador, à-peu-près à la moitiéde la hauteur du Vésuve, et à côté de couransrécens de laves, nous l’avons trouvée de 62° 15′;et enfin dans le cratère même du Vésuve, surdes scories, de 62° 0′. On voit donc que quoiqu’il y ait une différence dans la plupart deces inclinaisons, en les comparant les unes auxautres, elle n’est pas aussi grande que celleà laquelle on auroit pu s’attendre; et que, sile Vésuve a une influence sur l’inclinaison del’aiguille aimantée, elle est au moins très-petiteet très-locale. Si, en effet, à l’hermitage deS.-Salvador, l’inclinaison est plus grande de40′ qu’à Naples, à Portici elle est de 35′ pluspetite. L’intensité paroît avoir varié d’une manièreplus sensible et plus irrégulière. Quoique Naplessoit plus au midi que Rome, l’intensité y estplus grande d’un centième. A Portici elle estencore d’un quatre-vingt-onzième plus grandequ’à Naples, et à l’hermitage d’un quarante-cinquième. Mais dans le cratère du Vésuve,elle est au contraire d’un quinzième plus petite.Tant d’irrégularité et un décroissement si ra- |19| pide dans l’intensité, de la base du Vésuve àson sommet, prouvent que ce volcan ne peutêtre considéré comme un centre magnétiquedont l’influence s’étendroit au loin. Cette in-fluence paroît au contraire très-locale et doitdépendre entièrement de l’action de quelquesparties de laves un peu plus chargées de ferdans un endroit que dans un autre. Au milieudu cratère, comme nous étions immédiatementsur les scories, notre aiguille à oscillations ho-risontales a pu se trouver près d’une scoriemagnétique, dont les pôles auroient été placésen sens contraire des siens. Dans ce cas, onconçoit la diminution d’intensité que nous avonsobservée. Mais telle supposition qu’on fasse d’ail-leurs, on ne peut l’expliquer par l’incandescencedes matières que renferme le Vésuve. Car, s’ilest vrai que la chaleur détruise la force d’unaimant, un volcan n’est aussi qu’un point surle globe, et l’influence du noyau magnétiquepénétreroit dans son intérieur pour se pro-pager au-delà, de la même manière qu’ellepénètre et se propage dans l’espace au-delà dela surface de la terre. Considérons actuellement nos observationsd’une manière générale, depuis Berlin jusqu’àNaples. Nous verrons d’abord à la colonne des |20| tems, pour 60 oscillations horisontales, que letems diminue progressivement avec la latitude.A Berlin, il faut pour 60 oscillations 316″, 5;à Paris, il n’en faut que 314; à Milan, 295,5;à Rome, 281,8, et à Naples, 279,0. Il estdonc évident qu’à partir de Berlin, la forcehorisontale va en augmentant à mesure qu’ons’approche de l’équateur. Un accroissement sem-blable auroit toujours lieu, quelle que fût laloi de l’intensité de la force en raison de ladistance aux pôles; mais on peut concevoirune loi croissante de l’équateur magnétique auxpôles, telle qu’il y auroit un point intermé-diaire où la force horisontale seroit à son maximum. Il est possible que d’après la loi dumagnétisme terrestre, que nous ne connoissonspas encore, mais que nous savons croissantede l’équateur aux pôles, il existe un point sem-blable dont la position, si elle étoit bien connue,seroit utile dans la détermination de cette loi.D’après nos observations, ce point ne pour-roit se trouver qu’au-dessous de la latitude deNaples. Si on réduit les oscillations horisontales àcelles qui auroient lieu dans la vraie directiondes forces magnétiques, les intensités totalessuivent alors une loi différente; elles vont |21| en diminuant avec la latitude. En supposantl’intensité sous l’équateur magnétique égale à10000, elle est à Berlin 13703, à Paris 13482,à Lyon 13334, à Milan 13364, à Rome 12642,et enfin à Naples 12745. Ainsi la loi décou-verte par M. Humboldt, dans son voyage auxtropiques, de l’intensité croissante des forcesmagnétiques, en allant de l’équateur aux pôles,se trouve confirmée en Europe pour la France,l’Italie et l’Allemagne. Si nous considérons les inclinaisons, nousremarquerons qu’elles diminuent avec la la-titude d’une manière assez régulière. A Berlin,nous avons trouvé l’inclinaison de l’aiguille69° 53′; à Gottingen, 69° 29′; et M. Mayer,69° 26′; à Paris, 69° 12′; à Lyon, 66° 14′;à Milan, 65° 40′; à Rome, 61° 57′, et àNaples, 61° 35′. Les inclinaisons correspon-dantes données par la théorie, d’après M. Biot,sont toutes beaucoup plus grandes, car lesplus petites différences vont à près de 4°. Ensupposant la position de l’équateur magnétiquerigoureusement déterminée, il en résulteroitqu’en Europe il y a une inflexion considé-rable des parallèles magnétiques vers l’équa-teur, occasionnée par l’influence de quelquecentre particulier. Mais pour tirer aucune |22| conclusion à cet égard, il est prudent d’attendreque des observations exactes et plus nom-breuses fournissent des bases solides, sur les-quelles on puisse élever une théorie rigoureusequi les embrasse toutes.
|Tome I, page 22|
| LIEUXDESOBSERVATIONS. | LATITUDES mesuréesen degrésanciens. | LONGITUDESmesuréesen degrésanciens. | LATITUDES rapportéesà l’équateurmagnétique. | LONGITUDES orientalescomptéesdu nœudde l’équateurmagnétique,dansla mer du sud. | TEMS pour60 oscillationshorisontales. | FORCES magnétiquescomparéesà celle qui a lieusous l’équateurmagnétique,supposéeégale à 10000. | INCLINAISONSobservées. | INCLINAISONScalculées. | DIFFÉRENCES. | HAUTEURS en mètresdes lieuxau-dessusdu niveaude la mer. | NATUREDUSOL. |
| ° ′ ″ | ° ′ ″ | ° ′ ″ | ° ′ ″ | ° ′ | ° ′ | ° ′ ″ | ° ′ ″ | mètres. | |||
| Berlin.................. | 52.31.30 | 11.00.30 | 60.03.17 | 143.09.40 | 316.05 | 13703 | 69.53 | 73.55.54 | 4.02.54 | 26 | Sables qui couvrent lapierre calcaire. |
| Magdebourg............ | .......... | .......... | .......... | .......... | 316.05 | .......... | 69.35 | .......... | .......... | 76 | Grès. |
| Gottingen.............. | 51.32.05 | 07.33.00 | 59.36.15 | 138.34.40 | 316.02 | 13485 | 69.29 | 73.39.13 | 4.10.13 | 192 | Calcaire neuf. |
| Clèves................. | .......... | .......... | .......... | .......... | .......... | .......... | 70.08 | .......... | .......... | .......... | |
| Heidelberg............. | 49.24.30 | 06.21.23 | .......... | .......... | .......... | .......... | 68.39 | .......... | .......... | 132 | Granite. |
| Heilbronn.............. | .......... | .......... | .......... | .......... | .......... | .......... | 68.01 | .......... | .......... | 162 | Grès. |
| Paris.................. | 48.50.14 | .......... | 57.57.00 | 128.22.47 | 314.00 | 13482 | 69.12 | 72.62 00 | 3.50.00 | 40 | Gipse; calcaire de nouvelleformation. |
| Tübingen.............. | 48.31.04 | 06.43.15 | 56.46.36 | 136.20.20 | 305.02 | 13569 | 68.04 | 71.52.26 | 3.48.26 | 376 | Grès. |
| Wellendingen.......... | 48.08.49 | 06.22.15 | .......... | .......... | .......... | .......... | 67.57 | .......... | .......... | 440? | Calcaire du Jura. |
| Villeneuve-sur-Yonne.... | .......... | .......... | .......... | .......... | 306.04 | .......... | .......... | .......... | .......... | 95 | |
| Lucie-le-bois............ | .......... | .......... | .......... | .......... | .......... | .......... | 68.10 | .......... | .......... | .......... | |
| Zurich................. | 47.22.00 | 06.12.30 | 55.43.11 | 135.18.40 | 304.01 | .......... | 67.27 | .......... | .......... | 426 | Grès. |
| Lucerne................ | .......... | .......... | .......... | .......... | 301.04 | .......... | 67.10 | .......... | .......... | 450 | Idem. |
| Altorf.................. | .......... | .......... | .......... | .......... | 301.05 | 13228 | 66.53 | .......... | .......... | 494 | Calcaire de transition. |
| Ursern, pente septentrionle.du S.-Gothard........ | .......... | .......... | .......... | .......... | 302.02 | 13069 | 66.42 | .......... | .......... | .......... | Schiste micacé. |
| Hospice du S.-Gothard... | .......... | .......... | .......... | .......... | 299.04 | 13138 | 66.22 | .......... | .......... | .......... | Granite de nouvelle forma-tion. |
| Airolo, pente méridionaledu S.-Gothard........ | .......... | .......... | .......... | .......... | 297.03 | 13090 | 65.55 | .......... | .......... | .......... | Schiste micacé. |
| Como.................. | .......... | .......... | .......... | .......... | 298.08 | 13104 | 66.12 | .......... | .......... | 36 | Pierre calcaire de transition. |
| Lyon.................. | 45.45.52 | 02.29.09 | 54.37.42 | 130.22.52 | 296.04 | 13334 | 66.14 | 70.27.26 | 4.13.26 | 186 | Granite feuilleté. |
| Saint-Michel............ | 45.23.17 | .......... | .......... | .......... | 294.05 | 13488 | 66.12 | .......... | .......... | .......... | Schiste argileux de transi-tion. |
| Modane................ | .......... | .......... | .......... | .......... | .......... | .......... | 66.06 | .......... | .......... | .......... | Idem. |
| Lans-le-Bourg, au pied dumont Cénis........... | 45.17.40 | .......... | .......... | .......... | 297.01 | 13227 | 66.09 | .......... | .......... | .......... | |
| Hospice du mont Cénis... | 45.14.10 | .......... | .......... | .......... | 296.00 | 13441 | 66.22 | .......... | .......... | 2120 | Schiste micacé. |
| Turin................. | 45.04.14 | 05.20.00 | 53.35.00 | 133.31.09 | 295.00 | 13364 | 66.03 | 69.45.09 | 3.42.09 | .......... | Adossé à des montagnes deserpentine mêlée de dial-lage métalloïde. |
| Milan................. | 45.28.05 | 06.51.15 | 53.46.14 | 134.34.46 | 295.05 | 13121 | 65.40 | 69.52.49 | 4.12.49 | .......... | Sable qui couvre des rochesprimitives. |
| Pavie.................. | 45.10.47 | 06.49.33 | .......... | .......... | 291.05 | .......... | 65.26 | .......... | .......... | 86 | Idem. |
| Plaisance............... | 45.02.44 | 07.22.17 | .......... | .......... | .......... | .......... | 65.00 | .......... | .......... | .......... | |
| Parme........ ........ | 44.48.01 | 08.00.19 | .......... | .......... | .......... | .......... | 65.07 | .......... | .......... | .......... | |
| Modène................ | .......... | .......... | .......... | .......... | .......... | .......... | 64.55 | .......... | .......... | .......... | |
| Bologne............... | 44.29.36 | 09.00.15 | .......... | .......... | 290.03 | .......... | 64.48 | .......... | .......... | 124 | Grès nouveau. |
| Gênes................. | 44.25.00 | 06.38.00 | .......... | .......... | 295.00 | .......... | 64.45 | .......... | .......... | 16 | Calcaire de transition ausud de la Boguetta. |
| Rimini ................ | 44.03.43 | 10.12.36 | .......... | .......... | .......... | .......... | 63.48 | .......... | .......... | 6 | |
| Faenza................. | .......... | .......... | .......... | .......... | .......... | .......... | 63.54 | .......... | .......... | 20 | |
| Pezaro................. | 43.55.01 | 10.33.21 | .......... | .......... | .......... | .......... | 64.18 | .......... | .......... | 10 | |
| Florence............... | 43.46.30 | 08.55.00 | 51.49.28 | 137.15.45 | 290.00 | 12782 | 63.57 | 68.42.22 | 4.45.22 | 74 | Grès, grauwakke. |
| Spoleto................ | .......... | .......... | .......... | .......... | .......... | .......... | 62.51 | .......... | .......... | 280 | Calcaire du Jura. |
| Nocera................ | .......... | .......... | .......... | .......... | 285.04 | .......... | .......... | .......... | .......... | .......... | Idem. |
| Rome.................. | 41.53.54 | 10.07.30 | 49.48.50 | 138.03.49 | 281.08 | 12642 | 61.57 | 67.06.16 | 5.09.16 | 58 | Laves basaltiques, tuf, pé-périno mêlé de fermicacé. |
| Tivoli................. | .......... | .......... | .......... | .......... | 281.06 | .......... | .......... | .......... | .......... | 240 | Calcaire du Jura, tuf. |
| Naples ................. | 40.50.15 | 11.56.00 | 48.30.53 | 139.47.35 | 279.00 | 12745 | 61.35 | 66.08.54 | 4.33.54 | 16 | Tuf. |
| Portici, au pied du Vésuve. | .......... | .......... | .......... | .......... | 274.02 | 12883 | 60.50 | .......... | .......... | 20 | Laves. |
| L’hermitage de S.-Salvador,sur le flanc du Vésuve... | .......... | .......... | .......... | .......... | 279.00 | 13026 | 62.15 | .......... | .......... | .......... | Idem. |
| Cratère du Vésuve....... | .......... | .......... | .......... | .......... | 290.03 | 11933 | 62.00 | .......... | .......... | 1000 | Idem. |