Digitale Ausgabe
Download
| TEI-XML (Ansicht) | |
| Text (Ansicht) | |
| Text normalisiert (Ansicht) |
Ansicht
| Textgröße | |
| Originalzeilenfall ein/aus | |
| Zeichen original/normiert | |
Tafeln und Abbildungen
Zitierempfehlung
Alexander von Humboldt, Jean-Baptiste Biot: „Sur les variations du magnétisme terrestre à différentes latitudes“, in: ders., Sämtliche Schriften digital, herausgegeben von Oliver Lubrich und Thomas Nehrlich, Universität Bern 2021. URL: <https://humboldt.unibe.ch/text/1804-Sur_les_variations-1> [abgerufen am 24.04.2024].
URL und Versionierung
|
Permalink: https://humboldt.unibe.ch/text/1804-Sur_les_variations-1 |
| Die Versionsgeschichte zu diesem Text finden Sie auf github. |
| Titel | Sur les variations du magnétisme terrestre à différentes latitudes | ||||||
|---|---|---|---|---|---|---|---|
| Jahr | 1804 | ||||||
| Ort | Paris | ||||||
|
Nachweis in: Journal de physique, de chimie, d’histoire naturelle et des arts 59:6 (Frimaire an 13 [November/Dezember 1804]), S. 429–450, 3 Tafeln.
|
|||||||
| Beteiligte | Jean-Baptiste Biot | ||||||
|
Postumer Nachdruck Übersetzt als „Über die Veränderungen des Erdmagnetismus auf verschiedenen Breiten. Denkschrift von Humboldt und Biot. In der Klasse der mathematischen und physikalischen Wissenschaften des Nationalistituts von Biot gelesen am 17. Dezember 1804“ in: Heinz Balmer, Beiträge zur Geschichte der Erkenntnis des Erdmagnetismus, Aarau 1956, S. 495–520.
|
|||||||
| Sprache | Französisch | ||||||
| Typografischer Befund | Antiqua; Auszeichnung: Kursivierung; Fußnoten mit Ziffern; Tabellensatz; Formelsatz; Besonderes: mathematische Sonderzeichen. | ||||||
|
Identifikation |
|||||||
Statistiken
|
|||||||
| Weitere Fassungen | |
|---|---|
|
|
Sur les variations du magnétisme terrestre à différentes latitudes (Paris, 1804, Französisch) |
|
|
On the Variations of the Terrestrial Magnetism in different Latitudes (London, 1805, Englisch) |
|
|
Memoria sobre las variaciones del magnetismo terestre á diferentes latitudes (Madrid, 1805, Spanisch) |
|
|
Ueber die Variationen des Magnetismus der Erde in verschiedenen Breiten (Halle, 1805, Deutsch) |
SUR LES VARIATIONSDU MAGNÉTISME TERRESTRE À DIFFÉRENTES LATITUDES Par MM. HUMBOLDT et BIOT. Lu par M. Biot à la classe des Sciences mathématiques et physiques de l’Institutnational, le 26 frimaire an 13.
La recherche des lois du magnétisme terrestre est, sansdoute, une des questions les plus importantes que les physi-ciens puissent se proposer. Les observations déjà faites sur cetobjet ont découvert des phénomènes si curieux que l’on nepeut s’empêcher de chercher à résoudre les énigmes qu’ilsprésentent; mais malgré les efforts tentés jusqu’à ce jour,il faut avouer avec vérité que nous ne savons absolumentrien sur leurs causes. Il étoit difficile que l’on pût acquérir sur ce point des con-noissances bien précises, lorsque la construction des bous-soles étoit encore imparfaite, et il s’est écoulé si peu de tempsdepuis que les découvertes de M. Coulomb ont appris à lesrendre tout-à-fait exactes, qu’il ne faut pas s’étonner sil’on trouve jusqu’à présent peu de faits dignes d’une entièreconfiance dans les observations des voyageurs. L’expédition que M. Humboldt vient de terminer offre,pour cette partie de la physique, une collection non moinsprécieuse que celles dont il a enrichi les autres branches desconnoissances humaines; muni d’une excellente boussole d’in-clinaison construite par Le Noir, sur les principes de Borda,M. Humboldt a fait plus de trois cents observations sur l’in-clinaison de l’aimant, et sur l’intensité des forces magnéti-ques, dans la partie de l’Amérique qu’il a parcourue. Enjoignant à ces résultats ceux qu’il avoit déjà obtenus en Europe |430| avant son départ, on aura, pour la première fois, une suitede faits exacts sur la variation des forces magnétiques dansla partie boréale du globe, et dans quelques points de sapartie australe. L’amitié que M. Humboldt m’a témoignée depuis son retourm’ayant mis à portée de lui communiquer quelques expé-riences de ce genre, que j’ai faites cette année dans les Alpes,il m’offrit aussitôt de les réunir aux siennes dans le Mémoireque nous présentons aujourd’hui à la Classe: mais si le sen-timent de l’amitié, et le desir de connoître des phénomènesnouveaux, m’a fait accepter cette offre de M. Humboldt,la justice me défend d’en profiter à son préjudice, et je doisdéclarer ici le peu de part que j’ai dans ces observations. Pour mettre de l’ordre dans les faits et dans les conséquencesque l’on en peut déduire, il est nécessaire de considérerl’action du magnétisme terrestre sous divers points de vue,correspondans aux diverses classes de phénomèmes qu’elleproduit. Si nous la considérons d’abord en général, nousvoyons qu’elle agit sur toute la surface du globe terrestre,et qu’elle s’étend au-dehors dans l’espace. Ce dernier fait,qui avoit été révoqué en doute, a été prouvé depuis par unde nous, et sur-tout par notre ami M. Gay Lussac, dans lesdeux derniers voyages aréostatiques; et si ces observations,faites avec tout le soin possible, n’ont point laissé apercevoirde diminution sensible dans l’intensité des forces magnéti-ques à la plus grande hauteur où l’homme se soit jamaisélevé, on est en droit de conclure que cette force s’étendindéfiniment dans l’espace où elle décroît, peut-être, d’unemanière très-rapide, mais qui nous est jusqu’à présent in-connue. Si nous considérons maintenant le magnétisme, à la surfacemême de la terre, nous trouvons trois grandes classes dephénomènes qu’il est nécessaire d’étudier séparément, pouravoir une connoissance complète de sa manière d’agir. Cesphénomènes sont la déclinaison de la boussole, son inclinai-son et l’intensité de la force magnétique, considérées soitcomparativement dans les différens lieux, soit en elles-mêmesen ayant égard aux variations qu’elles éprouvent. C’est ainsiqu’après avoir reconnu l’action de la pesanteur comme uneforce centrale, on a ensuite constaté sa variation à différenteslatitudes, résultante de la figure de la terre. La déclinaison de la boussole paroît être jusqu’à présent |431| le phénomène qui a fixé plus particulièrement l’attention desphysiciens; sans doute à cause des secours que l’on espéroit entirer pour la mesure des longitudes; mais lorsque l’on sutque la déclinaison change dans le même lieu avec le temps,lorsqu’on eut remarqué ses variations diurnes, et ses affol-lemens irréguliers occasionnés par différens météores; enfin,la difficulté de l’observer sur mer à 1° près, on dut aban-donner cet espoir, et regarder la cause de ces phénomènescomme beaucoup plus compliquée, et plus profonde qu’onne l’avoit pensé d’abord. Quant à l’intensité des forces magnétiques dans les diffé-rentes parties du globe, elle n’avoit pas encore été mesuréed’une manière comparative. Les observations de M. Humboldt sur cet objet, découvrent un phénomène très-remarquable;c’est la variation de l’intensité à différentes latitudes, et sonaccroissement en allant de l’équateur aux pôles. En effet, la même boussole qui, lors du départ de M. Hum-boldt, donnoit à Paris 245 oscillations en 10 minutes de temps,n’en a plus donné au Pérou que 211, et elle a constammentvarié dans le même sens, c’est-à-dire, que le nombre desoscillations a toujours diminué en s’approchant de l’équateur,et toujours augmenté en s’en éloignant vers le nord. On ne peut pas attribuer ces différences à une diminutionde forces dans le magnétisme de la boussole, ni supposerqu’elle se seroit affoiblie par l’effet du temps et de la chaleur.Car après trois années de séjour dans les pays les plus chaudsde la terre, cette même boussole a donné de nouveau auMexique des oscillations aussi rapides qu’à Paris. On ne peut pas non plus révoquer en doute la justessedes observations de M. Humboldt, car il a souvent observéles oscillations dans le plan du méridien magnétique, et en-suite dans le plan vertical perpendiculaire à ce méridien:or en décomposant la force magnétique dans ce dernier plan,et la comparant à son action totale qui s’exerce dans le pre-mier, on peut d’après ces données calculer sa direction, etparconséquent la direction de l’aiguille (1). Cette inclinaison
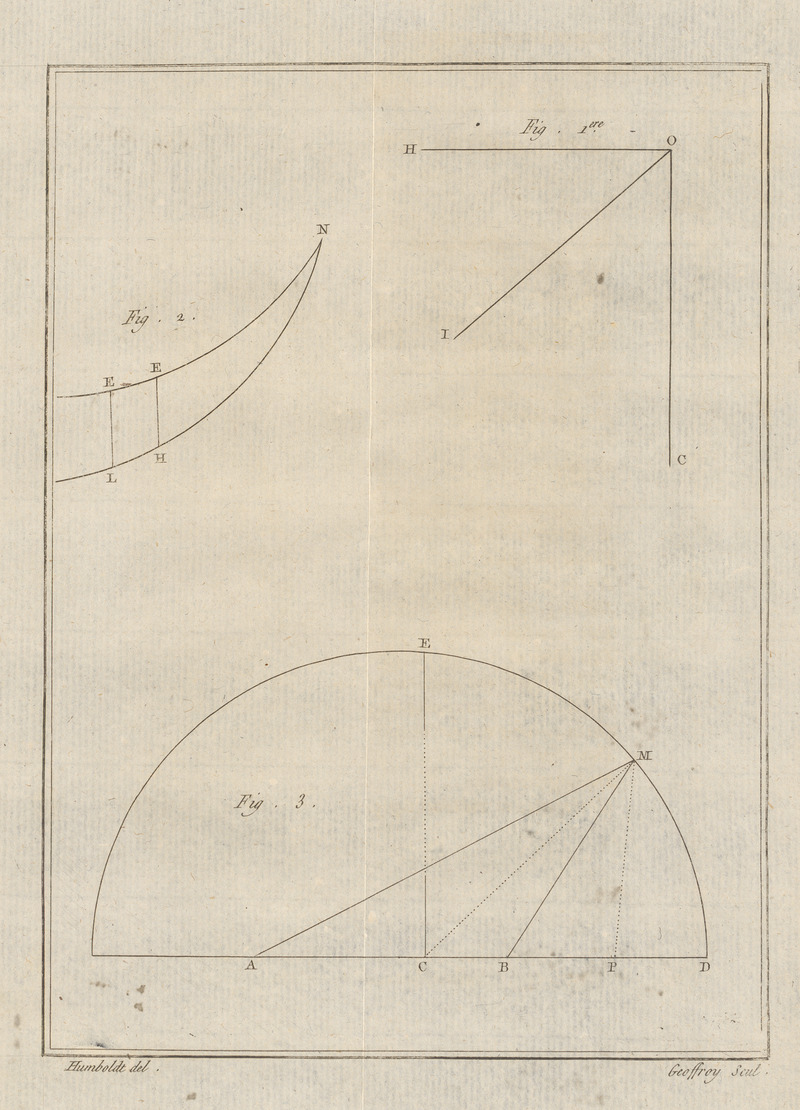
(1) Soit HOC (fig. 1), le plan du méridien magnétique qui passe la verti-cale OC, soit OL la direction de l’aiguille située dans ce plan, et OH unehorisontale. L’angle LOH sera l’inclinaison de l’aiguille, que nous désignerons|432| ainsi calculée se trouve toujours conforme à celle queM. Humboldt a observée directement. Cependant, lorsqu’ila fait ces expériences il ne pouvoit pas prévoir qu’on leurferoit subir cette épreuve, par laquelle M. La Place a imaginéde les vérifier. La justesse de ces observations ne pouvant pas être con-testée, il faut accorder aussi la vérité du résultat qu’ellesindiquent, et qui est l’accroissement de la force magnétiqueen allant de l’équateur vers les pôles. Pour suivre ces résultats avec plus de facilité, il convientde partir d’un terme fixe, et il paroît naturel de choisir pourcela les points où l’inclinaison de l’aiguille aimantée est nulle,parcequ’ils semblent indiquer les lieux où les actions opposéesdes deux hémisphères terrestres sont égales entr’elles. Lasuite de ces points forme sur la surface de la terre une lignecourbe qui diffère très-sensiblement de l’équateur terrestre,dont elle s’écarte au midi, dans l’Océan atlantique, et au norddans la mer du sud. On a nommé cette courbe l’équa-teur magnétique par analogie avec l’équateur terrestre, quoi-qu’on ne sache pas jusqu’à présent si elle forme précisémentun grand cercle sur le globe. Nous examinerons plus bascette question; mais pour le moment il nous suffit de dire,qu’au Pérou, M. Humboldt a rencontré cet équateur vers7°,7963 (7°. 1′) de latitude australe, ce qui le place, pour
par I. Si l’on nomme F la force magnétique totale qui agit suivant OL, lapartie de cette force qui agit suivant OC, sera F sin I: or les forces magné-tiques qui déterminent les oscillations de l’aiguille dans un plan quelconque,sont entr’elles comme les quarrés des nombres d’oscillations faites dans lemême temps. Si donc on désigne par M le nombre des oscillations faites en10′ de temps dans le méridien magnétique, et par P le nombre des oscilla-tions aussi faites en 10′ dans le plan perpendiculaire, on aura la proportion \( \frac{F\;\text{sin.}\;I}{F}=\frac{P^{2}}{M^{2}} \), d’où l’on tire \( \text{sin.}\;I=\frac{P^2}{M^2} \). On peut donc calculer l’inclinaison par cette formule, quand on a les oscil-lations faites dans les deux plans.On pourrait de même, en faisant osciller successivement une aiguille dansplusieurs plans verticaux, déterminer la direction du méridien magnétique.|433| cette partie de la terre, à-peu-près à l’endroit où Wilke et Lemonnier l’avoient mis. Les lieux situés au nord de ce point peuvent se partageren quatre zônes, dont les trois premières, plus rapprochéesde l’équateur, ont environ 4°,5 (4°) de largeur en latitude,tandis que la dernière, plus étendue et plus variable, ena 16° (14°). De sorte que le système de ces zônes s’étenddans l’Amérique, depuis l’équateur magnétique, jusqu’à25°,5556 (23°) de latitude boréale, et embrasse en longitudeun intervalle d’environ 56° (50°). La première zône s’étend depuis 7°,7963 (7°,1′) de latitudeaustrale, jusqu’à 3°,22 (2°,54′). Le nombre moyen des oscil-lations de l’aiguille dans le méridien magnétique en 10′ detemps, y est de 211,9; aucune observation n’en présentemoins de 211 ni plus de 214: on pourroit, d’après les obser-vations de M. Humboldt, former une zône semblable du côtéaustral de l’équateur magnétique, elle donneroit les mêmesrésultats. La deuxième zône s’étend depuis 2°,4630 (2°,13′) de lati-tude australe, jusqu’à 3°,61 (3°,15′) de latitude boréale.Le terme moyen des oscillations y est de 217,9; aucune n’estau-dessous de 214, ni au-dessus de 223. La troisième zône s’étend depuis 5° (4°,36′) à 9°,9259(8°,56′) de latitude boréale. Le terme moyen des oscillations yest de 224; aucune n’est au-dessous de 220, ni au-dessusde 226. Enfin la quatrième zône, plus large que les deux autres,s’étend depuis 10°,2778 (9°,15′), jusqu’à 25°,7037 (23°,8′)de latitude boréale. Son terme moyen est de 237; elle neprésente aucune observation au-dessous de 229, ni au-dessusde 240. On ignore, pour cette partie de la terre, l’intensité desforces magnétiques au-delà de 26° (23°) de latitude boréale,et au contraire, dans notre Europe, où l’on a des observa-tions faites à de hautes latitudes, on n’en a point aux en-virons de l’équateur; mais nous ne nous hasarderons pointà comparer ces deux classes d’observations qui peuvent ap-partenir à différens systèmes de forces, comme nous le dironsplus bas. Quoi qu’il en soit, le seul rapprochement des résultatsrecueillis en Amérique par M. Humboldt nous paroît établiravec certitude l’accroissement des forces magnétiques de l’é- |434| quateur aux pôles, et sans vouloir les lier de trop près avec lesexpériences que l’on a faites en Europe, nous devons cependantremarquer que celles-ci s’accordent également avec les pré-cédentes pour indiquer ce phénomène. Si nous avons ainsi partagé les observations par zônesparallèles à l’équateur, c’est pour mieux faire ressortir lavérité du fait qui en résulte, et sur-tout c’est pour en rendrela démonstration indépendante des petites anomalies qui semêlent inévitablement à ces résultats. Quoique ces anomalies soient fort légères, elles sont ce-pendant assez sensibles et assez fréquentes, pour qu’on nepuisse pas les attribuer tout entières aux erreurs des obser-vations. Il paroît plus naturel de les attribuer à l’influencedes circonstances locales, et aux attractions particulièresexercées par les amas de matières ferrugineuses, par leschaînes de montagnes ou par les grandes masses des con-tinens. En effet, l’un de nous ayant emporté, cet été, dans lesAlpes, l’aiguille aimantée dont il avoit fait usage dans unedes dernières ascensions aérostatiques, il a trouvé que satendance à revenir au méridien magnétique étoit constam-ment plus forte dans ces montagnes qu’elle ne l’étoit à Parisavant son départ, et qu’elle ne s’est trouvée depuis son re-tour. Cette aiguille qui faisoit d’abord à Paris 83°,9 en 10minutes de temps, a varié ainsi qu’il suit dans les différenslieux où on l’a transportée.
| LIEUX des observations. | Nombre des oscillationsen 10′ de temps |
| Paris avant le départ...... | 83,9 |
| Turin............. | 87,2 |
| Sur le mont Genêvre...... | 88,2 |
| Grenoble........... | 87,4 |
| Lyon............. | 87,3 |
| Genève............ | 86,5 |
| Dijon............. | 84,5 |
| Paris, au retour........ | 83,9 |
(1) Pour calculer cette position, soit NEE′ l’équateur terrestre (fig. 2), NHL l’équateur magnétique supposé aussi un grand cercle, et HL les deux points|438| Nous ne donnons pas cette détermination comme rigoureu-sement exacte; on pourroit sans doute y faire quelques cor-rections si l’on avoit un plus grand nombre d’observationségalement précises; mais nous croyons cependant que ces cor-rections seroient fort petites, et l’on verra plus bas qu’indé-pendamment de la confiance que méritent les deux observa-tions dont nous avons fait usage, nous avons encore d’autresraisons de penser ainsi (1).
de cet équateur que MM. Humbold et Lapeyrouse ont observés. On connaît leslatitudes HE, LE′ et l’arc EE′ qui est la différence des longitudes de ces deuxpoints. Parconséquent si l’on suppose HE = b, LE′ = b′, EE′ = v, EN = x et l’angle ENH = y, on aura deux triangles sphériques NEH, NE′L qui don-neront les deux équations \( \text{sin.}\;x=\frac{\text{tang.}\;b\;\text{cot.}\;y}{R} \) \( \text{sin.}\;(x+v)=\frac{\text{tang.}\;b'\;\text{cot.}\;y}{R} \), d’où l’on tire \( \frac{\text{sin.}\;(x+v)}{\text{sin.}\;{x}}=\frac{\text{tang.}\;b'}{\text{tang.}\;b} \), et en développant \( \text{cot.}\;x=\frac{\text{tang.}\;b'}{\text{tang.}\;b\;\text{sin.}\;v}-\frac{\text{cos.}\;v}{\text{sin.}\;v} \) prenons un angle auxiliaire φ tel que l’on ait \( \text{tang.}\;\phi=\frac{\text{tang.}\;b\;\text{sin.}\;v}{\text{tang.}\;b'} \), et il viendra \( \text{tang.}\;x=\frac{\text{sin.}\;v\;\text{sin.}\;\phi}{\text{sin.}\;(v-\phi)} \). Avec ces deux équations on calculera x, et l’on trouvera ensuite y, par une quel-conque des deux premiers.(1) Depuis la lecture de ce Mémoire, nous avons recueilli de nouveaux ren-seignemens qui confirment ces premiers résultats. Lapeyrouse, après avoir doubléle cap Horn, a rencontré une seconde fois l’équateur magnétique, par 18′ delatitude nord, et 119° 7′ de longitude, à l’occident de Paris. Il étoit donc alorsfort près du nœud de l’équateur magnétique, tel que nous venons de le déduired’observations. Ce fait établit positivement deux conséquences importantes:c’est d’abord que les déterminations précédentes n’exigent que de fort petitescorrections; et en second lieu, que l’équateur magnétique est réellement ungrand cercle du globe terrestre, sinon exactement, du moins à fort peu près. (Note des Auteurs du Mémoire.) |439| Il est très-remarquable que cette détermination de l’équateurmagnétique s’accorde presque parfaitement avec celle qui aété donnée depuis long-temps par Wilke et Lemonnier. Cedernier sur-tout qui, faute d’observations directes, avoit dis-cuté un grand nombre d’observations correspondantes, indiquel’équateur magnétique au Pérou, vers 7° \( \frac{1}{3} \) de latitude australe,et M. Humboldt l’a trouvé dans le même lieu à 7°,7963 (7°,1′);de plus la carte de Lemonnier, ainsi que celle de Wilke, indi-quent pour l’inclinaison de l’équateur magnétique 12°,22(environ 11°), et ils placent le nœud vers 155°,56′ (140) delongitude occidentale, comptée du méridien de Paris. Seroit-cedonc par hasard que ces élémens trouvés depuis plus de 40 anss’accordent si bien avec les nôtres fondés sur des observationsrécentes, ou seroit-ce que l’inclinaison de l’équateur magné-tique sur l’équateur terrestre n’éprouve que de très-petitesvariations, tandis que tous les autres symptômes du magné-tisme terrestre changent si rapidement. On ne seroit paséloigné d’admettre cette dernière opinion, si l’on considèreque l’inclinaison de la boussole n’a pas changé à Paris de 3°depuis au moins 60 ans qu’on l’observe, et qu’à Londres,suivant les observations de Graham, elle n’a pas changé en200 de 2°, tandis que la déclinaison a varié de plus de 20°dans le même intervalle, et a passé de l’est à l’ouest: maisd’un autre côté l’observation de l’inclinaison est si difficile àfaire avec exactitude, et il y a si peu de temps qu’on sait la me-surer avec précision, qu’il est peut-être plus sage de s’abstenirde toute opinion prématurée sur des phénomènes dont lacause nous est totalement inconnue. Pour employer les autres observations de M. Humboldt surl’inclinaison, j’ai d’abord réduit les latitudes et les longitudesterrestres en latitudes et en longitudes rapportées à l’équa-teur magnétique, ces dernières étant comptées depuis le nœudde cet équateur dans la mer du sud. J’ai pu voir d’abordpar ces calculs que la position de ce plan, déterminée parnos recherches précédentes, étoit assez exacte: car des lieuxtels que Santa-Fé et Javita, où M. Humboldt avoit observé desinclinaisons à très-peu près égales, se sont trouvés à fort peuprès sur le même parallèle magnétique, quoique distans l’unde l’autre de plus de 6°,6666 (6°) en longitude (1).
(1) Ceci confirme encore ce que nous avons dit plus haut, que l’équateurmagnétique est sensiblement un grand cercle de la terre. (Note des Auteurs du Mémoire.) |440| Ces réductions faites, j’ai cherché à représenter la sériedes inclinaisons observées, et pour laisser au hasard aussipeu qu’il étoit possible, j’ai essayé d’abord une hypothèsemathématique assez conforme aux idée que l’on s’est faitesjusqu’à présent sur le magnétisme terrestre. J’ai supposé sur l’axe de l’équateur magnétique et à égaledistance du centre de la terre, deux centres de forces attrac-tives, l’un austral, et l’autre boréal, de manière à représenterles deux pôles magnétiques opposés du globe terrestre. J’aiensuite calculé l’effet qui devoit résulter de l’action de cescentres sur un point quelconque de la surface de la terre, enfaisant varier leur force attractive réciproquement au quarréde la distance, et j’ai ainsi obtenu la direction de la résultantede leurs forces, direction qui devoit être aussi celle de l’aiguilleaimantée à cette latitude. Voici le détail de ce calcul: Je suppose que le point B (fig. 3) soit le pôle magnétiqueboréal de la terre, et que le point A soit le pôle magnétiqueaustral. Je suppose qu’il y ait au point M, à la surface de laterre, une molécule de fluide austral qui soit attirée par B etrepoussée par A, en raison inverse du quarré de la distance,et je demande quelle sera la direction de la résultante des deuxforces dont cette molécule est animée. Il est évident que cettedirection sera aussi celle que prendroit au point M une aiguillede boussole suspendue librement; car à cause de la petitessede l’aiguille, par comparaison avec le rayon de la terre, leslignes menées de ses points à un même centre B ou A, peuventêtre censées parallèles, sur-tout si les points A et B sont prèsdu centre de la terre, ce qui est le cas de la nature comme onva le voir. Je supposerai d’abord que la terre a une figure sphérique etque les deux pôles A et B sont égaux en force. J’examineraiensuite jusqu’à quel point cette dernière supposition s’accordeavec les résultats observés, soient donc AM = D′, BM = D, CP = x, PM = y, l’angle MCP = u, CA = CB = a, et je ferai a = Kr, r étant le rayonde la terre, et K une constante indéterminée. Soient de plus X, Y, les forces qui sollicitent M parallèle- |441| ment aux axes des co-ordonnées, et β l’angle que la directionde la résultante fait avec l’axe ABC. On aura d’abord ces équations, ou F est la force magnétiqueà une distance égale à l’unité. \( X=\frac{F}{D^2}\;\text{cos.}\;MBD-\frac{F}{D'^2}\;\text{cos.}\;MAD \) ; \( D'^2=y^2+(x+a)^2=r^2+2\;\text{ax.}+a^2 \) \( Y=\frac{F}{D^2}\;\text{sin.}\;MBD-\frac{F}{D'^2}\;\text{sin.}\;MAD \) ; \( D^2=y^2+x-a)^2=r^2-2\;\text{ax.}+a^2 \), ou en mettant pour les cosinus leurs valeurs: \( X=\frac{F(x-a)}{D^3}-\frac{F(x+a)}{D'^3} \) \( Y=\frac{Fy}{D^3}-\frac{Fy}{D'^3} \) et comme on a \( \text{tang.}\;\beta=\frac{Y}{X} \), on aura aussi \( \text{tang.}\;\beta=\frac{\frac{y}{D^3}-\frac{y}{D'^3}}{\frac{x-a}{D^3}-\frac{x+a}{D'^3}}=\frac{y(D'^3-D^3)}{x(D'^3-D^3)-a(D'^3+D^3)} \) ou, en mettant pour x, y et a leurs valeurs r cos. u; r sin. u; Kr; \( \text{tang.}\;\beta=\frac{\text{sin.}\;u}{\text{cos.}\;u-K\left(\frac{D'^3+D^3}{D'^3-D^3}\right)} \); \( D'^2=r^2(1+2K\;\text{cos.}\;u+K^2) \); \( D^2=r^2(1-2K\;\text{cos.}\;u+K^2) \); ce qui donne enfin le système des deux équations \( \text{tang.}\;\beta=\frac{\text{sin.}\;u}{\text{cos.}\;u-K\left(\frac{D'^3+D^3}{D'^3-D^3}\right)} \) \( K\left(\frac{D'^3+D^3}{D'^3-D^3}\right)=\frac{(1+2K\;\text{cos.}\;u+K^2)^\frac{3}{2}+(1-2K\;\text{cos.}\;u+K^2)^\frac{3}{2}}{(1+2K\text\;{cos.}\;u+K^2)^{\frac{3}{2}}-(1-2K\;\text{cos.}\;u+K^2)^\frac{3}{2}}K \). |442| Ces équations déterminent la direction de l’aiguille aimantéerelativement à chaque point M, dont on connoît la distanceà l’équateur magnétique; mais on voit que cette directiondépend de la quantité K, qui représente la distance des centresmagnétiques au centre de la terre, cette distance étant expri-mée en parties du rayon terrestre. Il faut donc avant tout dé-terminer cette quantité d’après les observations. Pour le faire d’une manière approchée, et prendre ainsi unepremière idée de la valeur de K, j’ai choisi une observationfaite par M. Humboldt à Carichana, par 7°,2978 (6°,34′,5″) delatitude boréale comptée de l’équateur terrestre, et 78°,1111(70°,18′) de longitude occidentale comptée du méridien deParis, ce qui donne 16°,526 (14°,52′,25″) de latitude relative-ment à l’équateur magnétique, et 53°,7390 (48°,21′,53″) delongitude orientale à partir du nœud de cet équateur avecl’équateur de la terre. L’inclinaison de l’aiguille aimantée aété observée dans ce lieu par M. Humboldt, dans le mois demessidor de l’an 8, et il l’a trouvée égale à 33°,78 (divisioncentig.) (1). La comparaison de ce résultat avec les autresobservations de M. Humboldt, fait voir qu’on peut en effetle regarder comme convenant à cette latitude. Pour en faire usage j’ai donné successivement à K diversesvaleurs dans la formule; j’ai calculé les inclinaisons qui enrésultoient à cette latitude, et en comparant ces résultats aveccelui que M. Humboldt avoit réellement observé, la marchedes erreurs m’a conduit naturellement vers la supposition laplus convenable. Voici le tableau de ces essais.
| Valeurs de K. | Inclinaisons de l’aiguille. | Erreurs. |
| K = 1 | 7°,73 | 26°,04 |
| K = 0,6 | 18°,80 | 14°,97 |
| K = 0,5 | 22°,04 | 11°,73 |
| K = 0,2 | 29°,38 | 4°,39 |
| K = 0,1 | 30°,64 | 3°,13 |
| K = 0,01 | 31°,04 | 2°,73 |
| K = 0,001 | 31°,07 | 2°,7 |
(1) Toutes les mesures d’inclinaison que je rapporterai dans ce Mémoire serontexprimées, comme celles de M. Humboldt, en parties décimales du quart decercle.|443| La première valeur de K placeroit les centres des forcesmagnétiques à la surface même de la terre, et aux pôles del’équateur magnétique; on voit que cette supposition ne sau-roit être admise, parcequ’elle donneroit un accroissementd’inclinaison beaucoup moins rapide que celui qui est indiquépar les observations. Il en est de même des résultats suivansqui placent les centres d’action sur le rayon terrestre, àdiverses distances du centre de la terre; mais on voit aussi engénéral qu’ils approchent de plus en plus de la vérité, àmesure que cette distance devient moindre, ce qui indiqueévidemment que les deux centres d’action des forces magné-tiques sont situés très-près du centre de la terre. Toutes lesautres observations de M. Humboldt conduiroient de même àcette conséquence. La supposition la plus convenable seroit donc de faire K nul,ou si petit qu’il devînt inutile d’y avoir égard; ce qui revientà regarder les deux centres d’action comme placés pour ainsidire dans une même molécule. En effet, le résultat obtenude cette manière est le plus exact de tous: il est égal à31°,0843; cette valeur est encore un peu moindre que celleque M. Humboldt a observée, et la différence est égale à2°,69; mais il faut considérer aussi que la formule d’où noustirons ces valeurs, suppose la position de l’équateur magné-tique parfaitement déterminée: or elle pourroit ne pas l’êtreavec la dernière exactitude, d’après les deux seules observa-tions de Lapeyrouse et de M. Humboldt dont nous avons faitusage. C’est donc en étudiant la marche de la formule, en lacomparant aux observations que nous pourrons apprécier sajustesse; après quoi nous pourrons songer à remédier auxpetites erreurs qu’elle peut encore entraîner. Pour parvenir au résultat que je viens d’indiquer, et qui estcomme la limite de tous ceux que l’on peut obtenir en don-nant à K diverses valeurs, il faut remarquer que la quantité \( K\left(\frac{D'^3+D^3}{D'^3-D^3}\right) \) ou \( K\cdot\frac{(1+2K\;\text{cos.}\;u+K^2)^\frac{3}{2}+(1-2K\;\text{cos.}\;u+K^2)^\frac{3}{2}}{(1+2K\;\text{cos.}\;u+K^2)^\frac{3}{2}-(1-2K\;\text{cos.}\;u+K^2)^\frac{3}{2}} \) devient \( \frac{0}{0} \) quand K est nul; mais en lui appliquant les métho- |444|des connues, on trouvera que sa valeur dans cette suppositionest réellement déterminée et égale à \( \frac{1}{3\;\text{cos.}\;u} \). En la substituantdans la formule, il vient \( \text{tang.}\;\beta=\frac{\text{sin.}\;u}{\text{cos.}\;u-\frac{1}{3\;\text{cos.}\;u}} \) équation qui peut être mise sous la forme \( \text{tang.}\;\beta=\frac{\text{sin.}\;2u}{\text{cos.}\;2u+\frac{1}{3}} \). Elle donnera facilement la valeur de β, et quand cette valeursera connue, on aura l’inclinaison I par la formule \( I=100+u-\beta \), qui servira dans toute l’étendue des deux hémisphères. D’après la marche que je viens de tracer, on voit que laformule précédente n’est pas simplement une constructionempyrique des observations, elle en est au contraire tout-à-fait indépendante, et elle suppose seulement l’inclinaison del’aiguille aimantée produite par l’action d’un aimant infini-ment petit, placé au centre de la surface terrestre: or encalculant d’après cette formule les inclinaisons pour diffé-rentes latitudes, j’ai trouvé précisément les mêmes nombresque M. Humboldt a observés soit en Europe, soit en Amé-rique, et ce ne sont pas seulement ses observations qui setrouvent représentées de cette manière; mais celles qui ontété faites en Russie et à Kola, en Laponie, lors du dernierpassage de Vénus, sont aussi comprises dans la même loi.C’est ce que prouve le tableau joint à ce Mémoire, où j’ai calculéles observations de Mallet et de Pictet, avec une partie de cellesde M. Humboldt que j’ai prises au hasard, mais cependantde manière à embrasser toutes les autres dans leurs inter-valles. On voit que les résultats de la formule s’écartent très-peudes observations; mais ces differences peuvent être renduesencore plus petites. En effet, en examinant la marche des |445| erreurs, on voit que les nombres donnés par le calcul, sont unpeu trop foibles en Amérique pour les petites latitudes, etun peu trop forts dans les latitudes élevées, ce qui indiqueque l’on pourra tout accorder par quelques légères modifica-tions, soit en changeant tant soit peu le nœud et l’inclinai-son de l’équateur magnétique, que deux observations nepeuvent pas déterminer avec la dernière exactitude; soit endéplaçant un peu notre petit aimant, en laissant toujours soncentre dans le plan de l’équateur magnétique, et le plaçant demanière qu’il soit un peu plus près de l’Amérique que del’Europe. Ce sont les observations mêmes, quand nous enaurons un plus grand nombre, qui devront nous guider dansces petites corrections. Au reste il ne faut pas s’attendre à représenter rigoureuse-ment par une loi mathématique toutes les inclinaisons obser-vées; car le phénomène de l’inclinaison, quoique plus régu-lier que les autres effets magnétiques, n’est pas exempt dequelques anomalies; c’est ce que l’on peut aisément voir enconstruisant la courbe donnée par les observations mêmes.Ainsi, par exemple, l’inclinaison observée à Popayan est de0°,10 plus forte qu’à St-Carlos Del Rio Negro, quoique lalatitude magnétique de ce second lieu soit de 0°,6852 (3°,7′)plus considérable. Il en est de même des observations faitesà Javita et à Santa-Fé. D’autres anomalies se décèlent par lamarche comparée des observations et de la formule: c’est cequi arrive pour Carichana, St-Thomas de la Guyane, et Car-thagène des Indes; l’accroissement de l’inclinaison du pre-mier au second de ces points n’est nullement en harmonieavec l’accroissement du second au troisième, et si l’on com-pare entre elles les intensités observées dans ces différens en-droits, les anomalies qu’elles présentent, annoncent en quel-que sorte celles que l’inclinaison doit y éprouver. La cause de ces anomalies devient évidente d’après ce quenous avons remarqué plus haut; elles sont uniquement l’effetdes circonstances locales, et sont dues à de petits systèmesd’attraction qui modifient les phénomènes généraux. Celadoit être sur-tout sensible pour la partie de l’Amérique queM. Humboldt a parcourue, et qui est traversée dans toute salongueur par la grande chaîne de la Cordilière des Andes.C’est aussi dans ces lieux qu’existent les différences les plusconsidérables. Popayan, par exemple, est situé près des vol- |446| cans de Sotara et de Pouracé; il est adossé à des montagnesbasaltiques chargées de fer magnétique. Près de Sulumito, àl’est de Popayan, ces colonnes basaltiques ont des pôles très-marqués; de même le Mexique est situé à 1160t de hauteursur le dos de le grande cordilière de Lenschtitlan: le terreiny est couvert de basaltes et d’amigdaloïdes poreuses, qui sontpresque toutes chargées de fer magnétique. Toutes ces causesne doivent-elles pas influer sensiblement sur l’inclinaisonde l’aiguille aimantée, et la disposition différente des massesferrugineuses, ou leur changement d’état par suite des actionsde la nature, ne doivent-elles pas y produire aussi des varia-tions. M. Humboldt a fait sur ce point une observation déci-sive: le tremblement de terre du 4 novembre 1799, a changé àCamana l’inclinaison de l’aiguille; elle étoit le 1er novembrede 43°,65; le 7 elle n’étoit plus qu’à 42°,75, et 10 mois aprèselle revint à 42°,85, mais elle ne regagna plus son anciennevaleur: l’intensité des forces magnétiques n’avoit pas changépar l’effet de ce tremblement. Il est donc prouvé par ces diverses observations, que les cir-constances locales peuvent avoir sur l’inclinaison une influencesensible, et cette influence se fait remarquer dans les contréesque M. Humboldt a parcourues (1). Ainsi il paroît que l’hypothèse mathématique dont nousavons fait usage, exprime réellement la loi de la nature, dumoins au nord de l’équateur magnétique; car quoique lespremiers résultats observés du côté du sud paroissent s’y plierencore, l’incertitude où nous sommes relativement à la vraiecause de ces phénomènes, doit arrêter nos conjectures, etnous empêcher d’étendre trop loin les conséquences des loisque nous observons (2).
(1) Nous pouvons observer que les anomalies sont sur-tout sensibles dans lesîles. (Note des Auteurs du Mémoire.) (2) Depuis la lecture de ce Mémoire nous pouvons avancer quelque chose deplus positif. Les observations faites au cap de Bonne-Espérance, au cap Horn et àla Nouvelle-Hollande par divers navigateurs, sont très-exactement représentées parnotre formule, et il s’ensuit qu’elle s’étend aussi à l’hémisphère austral. Nous espéronsavoir bientôt des renseignemens nombreux et très-exacts sur l’inclinaison de l’ai-guille dans cette partie de la terre. Mais nous avons cru devoir joindre dès àprésent à notre tableau les résultats qui s’y rapportent et que nous avons punous procurer. Nous y avons inséré de plus deux observations de l’intensité,faites avec beaucoup de soin par M. Rossel, dans l’expédition d’Entrecasteaux:|447| D’après les résultats précédens on peut calculer les points oùl’axe de l’équateur magnétique perce la surface terrestre; carleurs latitudes sont égales au complément de l’obliquité de cetéquateur, et leur méridien est à 100° de longitude de ses nœuds.On trouve ainsi le pôle magnétique boréal à 97°,7975(79°,1′,4″) de latitude boréale, et à 33°,3719 (30°,2′,5″) delongitude à l’occident de Paris, ce qui le place au nord de l’Amérique. L’autre pôle magnétique, symétrique, au précé-dent, est situé à la même latitude australe, et à 66°,6281(149°,67′,55″) de longitude à l’orient de Paris, ce qui le placedans les glaces éternelles; indications tout-à-fait analogues àcelles de Wilke et de Lemonnier. Si l’on pouvoit arriver jusqu’à ces pôles, on y verroit laboussole verticale; mais si l’on peut accorder quelque con-fiance à la loi que nous venons de découvrir, ce seroit làl’unique différence qu’on y appercevroit relativement à l’in-clinaison, et l’on seroit encore aussi éloigné que dans notreEurope des véritables centres qui la produisent. Ce résultatparoîtroit de nature à diminuer l’intérêt que l’on pourroitavoir à visiter ces affreuses régions, si l’on n’avoit pas aussil’espoir d’y découvrir de nouveaux phénomènes relativementà l’intensité des forces magnétiques, et à l’influence desmétéores. Ces conséquences ne sont pas tout-à-fait d’accord avec l’opi-nion reçue assez généralement, et qui attribue l’augmentationdes effets magnétiques vers le nord, à la grande quantité demines de fer répandues dans ces régions; mais il nous sembleque cette opinion n’est pas conforme à la vérité. La cordilièredes Andes contient une énorme quantité de fer magnétique;le fer natif de Chaco, cette masse problématique analogue àcelle de Pallas, et celles de Xacateras, dans le Mexique, setrouvent sous les tropiques mêmes (1). En voyant les inclinaisons de la boussole si exactement re-presentées dans notre hypothèse, nous avons cherché si elle
observations très-importantes, parcequ’elles prouvent que la force du magné-tisme terrestre augmente aussi dans l’hémisphère austral à mesure que l’ons’éloigne de l’équateur. (Note des Auteurs du Mémoire.) (1) On peut maintenant ajouter aux considérations précédentes, ce fait décisif,que l’intensité augmente aussi lorsqu’on approche du pole austral. (Note des Auteurs du Mémoire.) |448| pourroit s’appliquer aussi aux intensités observées par M. Hum-boldt; mais nous avons vu qu’elle n’y satisfait pas. Elledonne bien, à la vérité, un accroissement de forces magné-tiques de l’équateur au pôle; mais cet accroissement d’abordtrop lent, est ensuite beaucoup trop rapide: je n’ai pas encorepu essayer si le petit déplacement de l’aimant terrestre con-tribuera à les mieux représenter, ou il faut remarquer que lasérie des intensités est extrêmement bisarre, et renferme uneinfinité d’anomalies, ensorte qu’il se pourroit que les circons-tances locales eussent, sur ce phénomène, une influence beau-coup plus sensible que sur l’inclinaison. En résumant les résultats que nous avons exposés dans ceMémoire, on voit que nous avons d’abord déterminé la posi-tion de l’équateur magnétique par des observations directes,ce qui n’avoit pas encore été fait. Nous avons ensuite prouvéque la force magnétique augmente en allant de cet équateurvers les pôles; enfin nous avons donné une hypothèse mathé-matique qui, réduite en formule, satisfait à toutes les incli-naisons observées jusqu’à présent. En supposant que nous ayons fait à cette formule les petitescorrections dont elle est susceptible, son utilité devient évi-dente, soit pour faire connoître par la suite des temps lesvariations qui peuvent survenir dans l’action du magnétismeterrestre, soit pour reconnoître, ou même prévoir la valeurde l’inclinaison, ce qui est d’une très-grande importance dansun grand nombre de cas. Par exemple, près de l’équateur magnétique, l’augmentationou la diminution de l’inclinaison indiquera à un bâtiment quifait son cours, s’il a gagné ou perdu en latitude par les courans.Cette connoissance de la latitude est quelquefois tout aussiimportante que celle de la longitude. Sur les côtes du Pérou,par exemple, les courans portent depuis Chiloé, avec unetelle force au nord et au nord-est, que l’on va de Lima à Guay-a-Quil en trois ou quatre jours, et qu’il faut deux, trois etquelquefois cinq mois pour en revenir. Il est parconséquent dela plus grande importance pour les bâtimens qui viennent duChili, longer la côte du Pérou, de connoître leur latitude.S’ils dépassent le port auquel ils sont destinés, ils ont à re-monter au sud, et chaque jour de marche exige souvent unmois de retour. Malheureusement les brumes qui règnent pen-dant quatre ou cinq mois sur les côtes du Pérou, empêchentde distinguer la configuration de la côte: on ne voit que la |449| cime des Andes et celle des pics qui s’élèvent au-dessus decette couche de vapeurs, mais dont la figure est trop uniformepour que le pilote puisse s’y reconnoître. Il reste souvent 12et 15 jours sans voir le soleil ou les astres, et pendant cetintervalle il se met à l’ancre, craignant de dépasser le port:mais si l’on suppose que l’on connoisse l’inclinaison de l’ai-guillé aimantée dans les ports qui sont au nord de Lima,par exemple à Chancay, Huaura et Santà, la boussole d’in-clinaison indiquera si l’on est, par rapport à Lima, au sud ouau nord. Elle apprendra même à-peu-près vis-à-vis quel pointde la côte on se trouve, et cette indication comporte même uneplus grande exactitude que l’on n’auroit osé l’espérer, parce-que, dans ces parages, l’inclinaison varie avec une rapiditéextraordinaire. M. Humboldt, à qui ces remarques appar-tiennent, a observé dans ces parages les valeurs suivantes:
| Lieux. | Latitudes australes. | Inclinaisons. |
| Huancey. | 10° 4′ | 6°,80 |
| Huaura. | 11° 3′ | 9°,00 |
| Chancay. | 11° 33′ | 10°,35 |
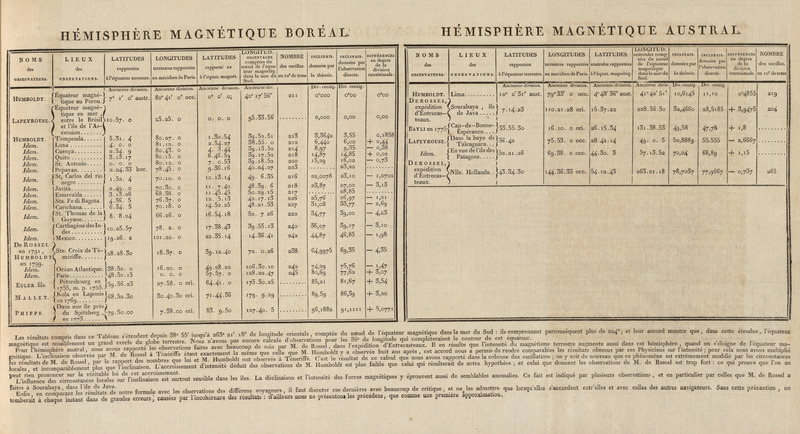
HÉMISPHÈRE MAGNÉTIQUE BORÉAL.
| NOMS des observateurs. | LIEUX des observations. | LATITUDES rapportéesà l’équateur terrestre. | LONGITUDES terrestres rapportéesau méridien de Paris. | LATITUDES rapporté esà l’équat. magnét. | LONGITUD. orientales comptées dunœud de l’équa-teur magnetiq.dans la mer duSud. | NOMBRE des oscillat.en 10′ de tems | inclinais. données parla théorie. | inclinais. données parl’observationdirecte. | différences en degrésde ladivisioncentésimale. |
| Ancienne division. | Ancienne division. | Ancienne division. | Ancienne div. | Div. centig. | Div. centig. | ||||
| Humboldt. | Équateur magné-tique au Pérou. | 7° 1′ 0″ austr. | 80° 4′ 0″ occ. | 0° 0′ 0; | 40° 17′ 56″ | 211 | 0°000 | 0°00 | 0°00 |
| Lapeyrouse. | Équateur magné-tique en mer,entre le Brésilet l’île de l’As-cension....... | 10.57. 0 | 25.25. 0 | 0. 0. 0 | 95.33.56 | ......... | 0,000 | 0,00 | 0,00 |
| Humboldt. | Tompenda...... | 5.31. 4 | 80.27. 0 | 1.30.54 | 39.52.51 | 213 | 3,3642 | 3,55 | 0,1858 |
| Idem. | Loxa .......... | 4. 0. 0 | 81.12. 0 | 2.54.27 | 38.55. 0 | 212 | 6,440 | 6,00 | + 0,44 |
| Idem. | Cuença ......... | 2.54. 9 | 80.43. 0 | 4. 3.44 | 39.13.52 | 214 | 8,97 | 9,35 | — 0,38 |
| Idem. | Quito .......... | 3.13.17 | 80.15. 0 | 6.46.59 | 39.17.52 | 218 | 14,87 | 14,85 | + 0.02 |
| Idem. | St. Antonio ..... | 0. 0. 0 | 80.12. 0 | 7. 0.53 | 39.18.52 | 220 | 15,29 | 16,02 | — 0,73 |
| Idem. | Popayan........ | 2.24.33 bor. | 78.45. 0 | 9.36.16 | 40.24.27 | 223 | ......... | 23,20 | ......... |
| Idem. | St. Carlos del rionegro ........ | 1.52. 4 | 70.10. 0 | 10.13.14 | 49. 6.35 | 216 | 22,0278 | 23,10 | — 1,0722 |
| Idem. | Javita.......... | 2.49. 0 | 70.30. 0 | 11. 7.40 | 48.39. 6 | 218 | 23,87 | 27,00 | — 3,13 |
| Idem. | Esmeralda ...... | 3.13.26 | 68.38. 0 | 11.45.45 | 50.29.15 | 217 | ......... | 28,85 | ......... |
| Idem. | Sta. Fe di Bagota. | 4.36. 5 | 76.37. 0 | 12. 5.13 | 42.17.13 | 226 | 25,76 | 26,97 | — 1,21 |
| Idem. | Carichana....... | 6.34. 5 | 70.18. 0 | 14.52.25 | 48.21.53 | 227 | 31,08 | 33,77 | — 2,69 |
| Idem. | St. Thomas de laGuyane....... | 8. 8.24 | 66.26. 0 | 16.54.18 | 52. 7.26 | 222 | 34,77 | 39,00 | — 4,23 |
| Idem. | Carthagène des In-des .......... | 10.25.57 | 78. 2. 0 | 17.38.43 | 39.55.13 | 240 | 36,07 | 39,17 | — 3,10 |
| Idem. | Mexico......... | 19.26. 2 | 101.22. 0 | 22.35.14 | 14.36.41 | 242 | 44,87 | 46,85 | — 1,98 |
| De Rossel en 1791, Humboldt en 1799. | Ste. Croix de Té-mériffe....... | 28.28.30 | 18.37. 0 | 39.12.40 | 72. 0.26 | 238 | 64,9975 | 69,35 | — 4,35 |
| Idem. | Océan Atlantique. | 38.52. 0 | 16.20. 0 | 49.28.22 | 106.30.10 | 242 | 74,29 | 75,76 | — 1,47 |
| Idem. | Paris........... | 48.50.15 | 0. 0. 0 | 57.57. 0 | 128.22.47 | 245 | 80,69 | 77,62 | + 3,07 |
| Euler fils. | Pétersbourg en1755, m. p. 1755. | 59.56.23 | 27.58. 0 ori. | 64.41. 0 | 173.30.25 | ......... | 85,21 | 81,67 | + 3,54 |
| Mallet. | Kola en Laponieen 1769......... | 68.52.30 | 30.40.30 ori. | 71.44.36 | 179. 9.29 | ......... | 89,59 | 86,39 | + 3,20 |
| Phipps. | Dans une île prèsdu Spitzberg,en 1773....... | 79.50.00 | 7.38.00 ori. | 83. 9.50 | 127.40. 5 | ......... | 96,1882 | 91,1111 | + 5,0071 |
HÉMISPHÈRE MAGNÉTIQUE AUSTRAL.
| NOMS des observateurs. | LIEUX des observations. | LATITUDES rapportéesà l’équateur terrestre. | LONGITUDES terrestres rapportéesau méridien de Paris. | LATITUDES australes rapportéesà l’équat. magnétiq. | LONGITUD. orientales comp-tées du nœudde l’équateurmagnétiquedans la mer duSud. | inclinais. données parla théorie. | inclinais. données parl’observationdirecte. | différences en degrésde ladivisioncentésimale. | NOMBRE des oscillat.en 10′ de tems |
| Ancienne division. | Ancienne division. | Ancienne division. | Ancienne divis. | Div. centig. | Div. centig. | ||||
| Humboldt. | Lima.......... | 12° 2′31″ aust. | 79°33′ 0 occ. | 4°48′36″ aust. | 41°42′51″ | 10,6145 | 11,10 | 0°4855 | 219 |
| Derossel, expéditiond’Entrecas—teaux. | Sourabaya, îlede Java ..... | 7.14.23 | 110.21.28 ori. | 15.37.22 | 228.56.50 | 32,4660 | 28,5185 | + 3,9475 | 204 |
| Bayli en 1775 | Cap-de-Bonne-Espérance.... | 33.55.30 | 16.10. 0 ori. | 26.15.34 | 131.38.53 | 49,58 | 47,78 | + 1,8 | ......... |
| Lapeyrouse. | Dans la baye deTalcaguara... | 36.42 | 75.53. 0 occ. | 28.42.14 | 49. 0. 5 | 52,8889 | 55.555 | — 2,6667 | ......... |
| Idem. | En vue de l’île desPatagons..... | 52.21.26 | 69.38. 0 occ. | 44.30. 3 | 57.13.52 | 70,04 | 68,89 | + 1,15 | ......... |
| Derossel, expéditiond’Entrecas—teaux. | Nlle. Hollande.. | 43.34.30 | 144.36.33 occ. | 54.12.43 | 263.21.18 | 78,7037 | 77.9667 | — 0,737 | 265 |